网络流
这里引入 dinic 模板和最经典的一类题型:等价于求二分图的最大匹配。而最大匹配用最大流来跑又快又好,并且还能顺便证明二分图最大匹配 = 最小点覆盖。
等价于二分图最大匹配¶
二分图中:最大匹配(最大流) = 最小点覆盖(最小割) = 点数 - 最大独立集
转换成二分图最大独立集。
这里我有点不确定选进来的是最大匹配还是最大权匹配。
特殊的二分图匹配¶
1009 未来城市 杭电联赛题 这题是特殊的二分图最大权匹配,但不适合跑费用流。
这里记一些比较简单的最大流、最小割的问题。
最大流¶
最小割¶
1006 发送他们房子 杭电联赛题
不考虑限制,即最小割
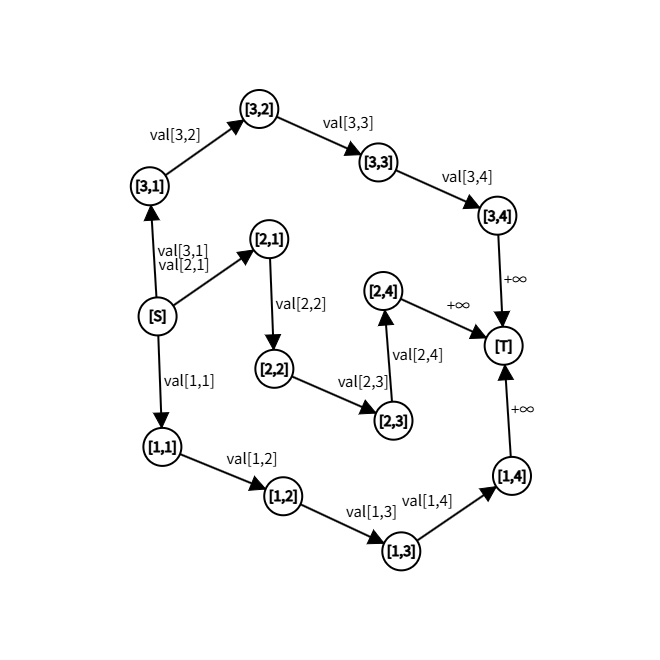
考虑限制,对于不能同时割掉的,即距离太远的两边,我们考虑一些“极小”的不可行区间,即对于任意不可行区间,都存在某个极小区间被其覆盖。比如上图中,假设 \([ [1,1],[2,3] ]\) 是一个极小区间,不符合限制,那么由于 \([ [1,1],[2,4] ] \supseteq [ [1,1],[2,3] ]\),自然也不符合限制。 或者说,不可行区间扩大后仍未不可行区间。被极小区间真包含的区间则是可行区间。这种性质允许我们按大小枚举左端点,右端点严格单调增直到这样的右端点不存在。 此外,不可行区间还有第一参数对称性。\([ [1,1],[2,3] ]\) 不可行的话,swap 两个位置的第一个参数,得到 \([ [2,1],[1,3] ]\),自然也是一个不可行区间。
延续上面段落的极小区间假设,现在我们希望断了 \([1,1]\) 和 \([2,3]\) 后,就不能得到最小割了。
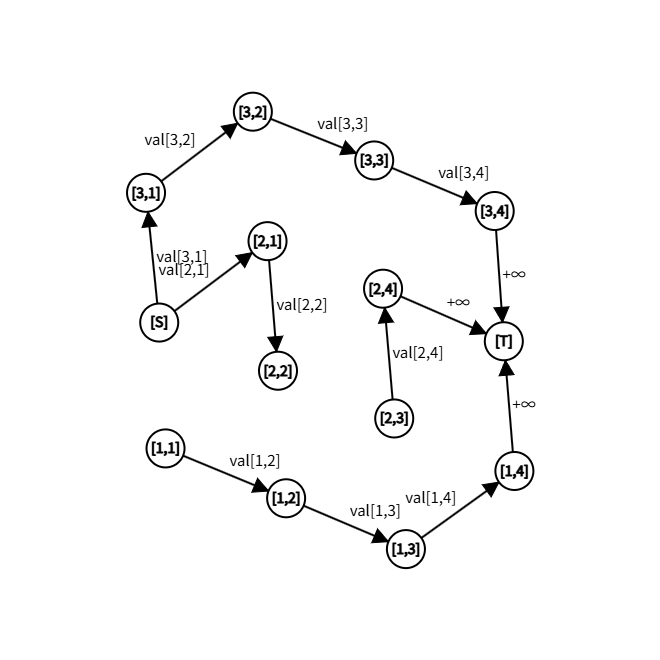
不仅如此,断掉 \([2,4]\) 也不允许。但是 \([2,2]\) 其实是允许的。那么我们就在这个边界上施加这样的约束
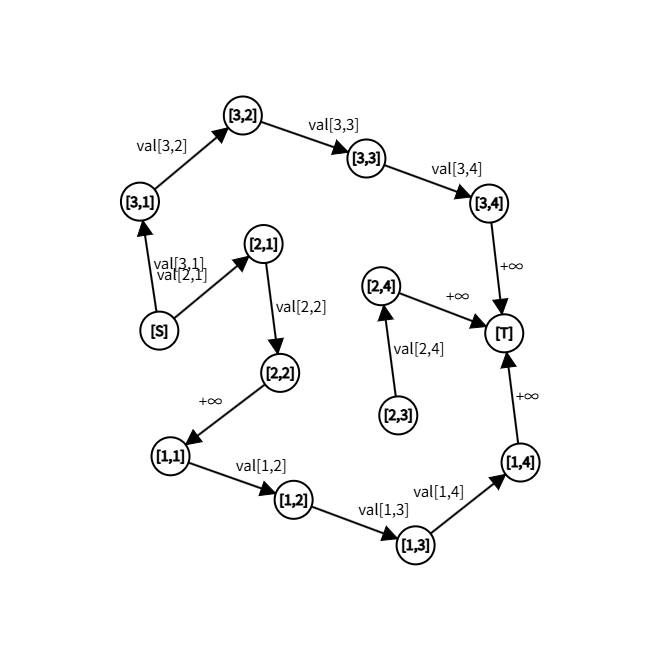
还原回去就是这样的 X 型回流无穷边支架。这种支架被激活的前提是:有一个割边跑到支架左边了,那么另一个割边必须严格在支架的左边,否则形成包含关系,这条割边就不够用,多割的这条必须在这条的左边,这时这条边去掉,就形成一个更小的割了。
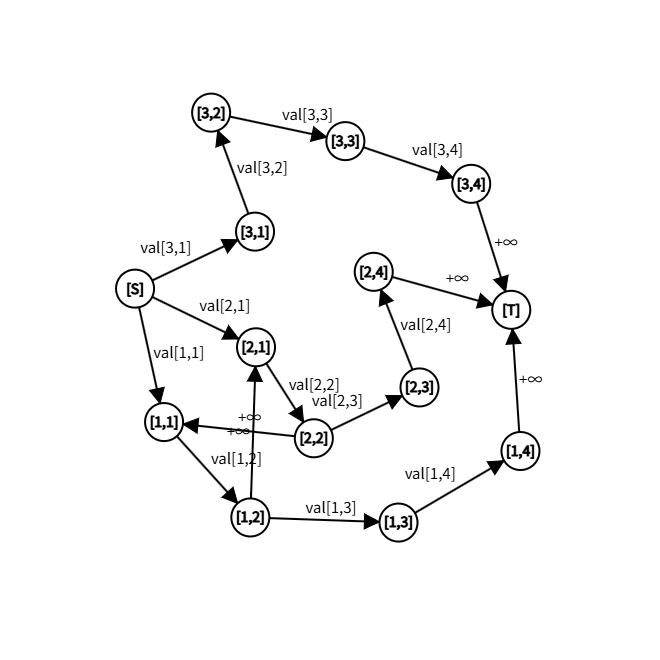
这里主要是费用流题单。费用流的流是不大的,一般一条边的流量只有 \(O(1)\) 拿来作约束。
网络流学习--费用流 - Manjusaka丶梦寒 - 博客园
费用流¶
挺有意思的,可以监测一个点的流量,建两条出边,一条边是 \([1,0]\),另一条是 \([1,p\cdot q]\), 如果这个点的流量是 \(1\),它只会走前面这条边,如果这个点的流量是 \(2\),它还会走后面这条边。
二叉树是入度为 1 出度为小于等于 2,这与网络流的流量约束并不完全一样。所以这里不能把 S 和 T 想象成树的一部分,而是分别管理出边和入边的约束。 拆点,一个点拆成两个点 \(u, v\),\(v\) 到 \(T\) 连 \([1,0]\),这条边上有流就代表它找到了唯一父亲,\(S\) 到 \(u\) 连 \([2,0]\) 代表最多找两个儿子,然后 \(u\) 连向所有可能成为儿子的 \(v'\) 以 \([1,\text{dis}_{u,v'}]\),如果上面有流就代表儿子找到了唯一父亲,父亲找到了一个儿子。
完整题面要结合看 802A
有一种不是特别模板,要控制增广次数,【CF802C】Heidi and Library (hard) 费用流 - CQzhangyu - 博客园。
好像还有一种建图是可以直接套模板的。如果没有复用书,晚卖(丢)不如早卖,也就是当天买当天卖,这样决策模型就简单一点。反之就对应到下一个位置,那个位置买入不用钱,卖出什么的就随便了。 然后考虑到虽然后面一个免费了,但是约束是针对前面的,所以可以连反向边,把贡献理解成后面占的便宜,进来的流量变成最后需要排出的约束。
可以稍微想一下,如果不拆点,就没法很好地把反向的意义(抵消后面的花费,同时给前面约束)和正向的意义(带着多余流量回到原来的地方)区分开来,甚至可能构成负环。所以我们在这里分出两层,层与层之间是单向的,层的意义是独立的。 下面是我的第一想法建模(有bug)和正解的建模。
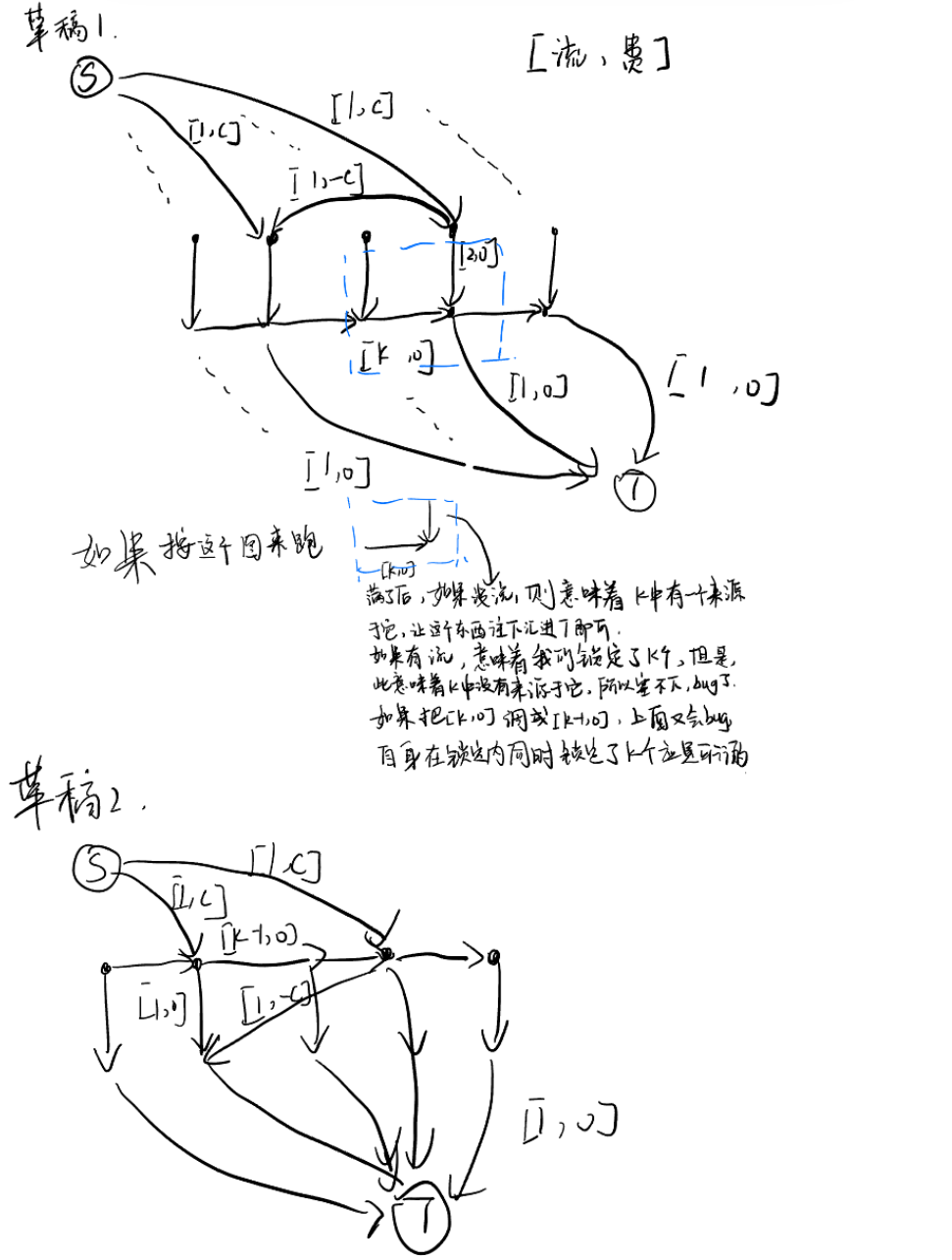
难题¶
此题单为较困难即 3000 分以上的题单,估计会鸽,只是作标记。
Problem - 2061H1 - Codeforces Problem - 2061H2 - Codeforces
题解 H2.pdf - Google 云端硬盘 Submission #302102508 - Codeforces 前面看出来是要检查 s 状态和 t 状态有没有 meet in the middle 的可能性,即它们至少能到达另一个状态。这个操作类似跑二分图匹配,可以建图最大流解决。 后面的这个东西为什么充分就很奇怪,没看懂题解什么意思。
basic notion¶
A graph \(G=(V,E)\), for every directed edge \(e_i\in E\), equipped with corresponding capacity \(c_i\) and flow \(f_i\) such that \(0\le f_i\le c_i\). Plus, we should assure that, except two special distinct points \(s,t\), how many flow in, how many flow out.
The overall flow \(||f||\) for the graph, which is a value, is defined as how many flow out from \(s\) (or equivalently, how many flow in to \(t\)) .
An s-t cut \(\{S,T\}\) divides \(V\) into two parts, and \(s\in S,t\in T\). When it comes to its value, we define it as $$ ||S,T||:=\sum_{u\in S}\sum_{v\in T} c(u,v) $$ Residue network flow just extract the flow right now, shift the capacity to make the flow seems like returning to \(0\). This model is easier to consider.
The equivalent "backflow" creating backward edges with no flow yet now and the capacity that how many flow out in the original direction. This is just a mark for the redistribution. Once we utilize them as part of augmentation, it's equivalent to say: Oh, the past one augmentation, please imagine you renege to do so on this single part, at the same time I'll keep the benifit you have get, at the same time I'll keep the restriction of being a flow. Whatever, the final state can be describe without any new edges at all, like the backflows have never existed.
An augmentation can be stated as, combine the technique of reneging, find a path from \(s\) to \(t\) and flow as much as possible. Obviously, it's the \(\max\) residue along the path. When the "much" can't be positive, it's said we can no longer augment the flow. Because the \(\max\) always choose integer, and the probable flow is a finite subset of integers, we can exhaustively do it in finite rounds.
flow always less than or equal to cut¶
the division idea to find the max¶
The motivation to consider this relationship, is somehow similar to Dedekind cut. Since cut always greater than flow, once the flow equals the cut, it should be the greatest among flows.
And by the above formalization, we can transform the possibility to whether the two inequality notations can be equal at the same time.
Intuitively, we need to verify NO \(T\) to \(S\) flows, and FULL \(S\) to \(T\) flows.
further construction for equality¶
The state that no longer can be augmented, which is mentioned can be reached in previous analysis, allows us to construct a extremely large \(S\), such that in the sense of residue network and backflow reneging, the \(||S,V\backslash S||'\) equals \(0\). That is to say, \(S\) will exhaustively absorb all the points yet outside, that have positive residue with the points already inside, including the reneging backflow. Since we can't augmented at all, the \(S\) can't including \(t\).
So the final result is, we have two distinct set which have fullfilled all the edges from \(u\mapsto v\), where \(u\in S,v\in T\) arbitrarily. If the edge is the original sense, FULL, this made the second inequality to be equal. Otherwise, is the backflow sense, the FULL actually representing the corresponding \(T\) to \(S\) flows are exhaustively reneging, so NO \(T\) to \(S\), made the first inequality to be equal.
In the future statement, we'll refer this as max-flow min-cut theorem.
instant application¶
Konig's theorem for bipartite graph¶
There is an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graph \((\{A,B\},E)\).
The trick here is very common in graph modeling. We add a source \(s\) and a sink \(t\) outside. Connecting the \(s\) to \(a\in A\) with capicity \(1\), the \(b\in B\) to \(t\) with capicity \(1\). and \(a\in A\) to \(b\in B\) with capicity \(+\infty\)(or a static but sufficiently large integer) if \((a,b)\in E\). The max-flow is equivalent to maximum matching, while the min-cut is equivalent to minimum vertex cover.
Menger's Theorem (edge version)¶
Tip: For undirected version, just split it into two ones, it still works. Then the modeling is trivial: assigning every edge with 1.